Unidad números
A continuación se presenta un vídeo de ayuda para recordar como resolver ejercicios con potencias


Unidad 1
OA1: Realizar cálculos y estimaciones que involucren operaciones con números reales:-Utilizando la descomposición de raíces y las las propiedades de las raíces.
-Combinando raíces con números racionales.
-Resolviendo problemas que involucren estas operaciones en contextos diversos.

Nosotros ya repasamos potencias y ahora comenzaremos a revisar la relación que existe entre la potencia y la raíz.
En el siguiente cuadro se muestra la relación que existe entre la potencia y la raíz.


EJEMPLOS DE ALGUNAS RAÍCES EXACTAS RESUELTAS

A continuación se presentan algunos ejercicios de raíces cuadradas exactas, encuentre su valor sin utilizar calculadora, de lo contrario la guía pierde sentido, debe recordar potencias, es decir buscar dos números iguales que multiplicados den la cantidad subradical (es decir la cantidad que está dentro de la raíz).

UNIDAD 1
OA1: Realizar cálculos y estimaciones que involucren operaciones con números reales:-Utilizando la descomposición de raíces y las las propiedades de las raíces.
-Combinando raíces con números racionales.
-Resolviendo problemas que involucren estas operaciones en contextos diversos.
A continuación se presenta un vídeo de propiedades de raíces
A continuación se presentan algunos ejercicios de la relación entre raíces y potencias, debes resolverlos en tu cuaderno

Como el desarrollo es en el cuaderno solo envía tus impresiones de como te resulto la actividad y que te pareció el vídeo que explica las propiedades
UNIDAD 1:
OA1: Realizar cálculos y estimaciones que involucren operaciones con números reales:-Utilizando la descomposición de raíces y las las propiedades de las raíces.
-Combinando raíces con números racionales.
-Resolviendo problemas que involucren estas operaciones en contextos diversos.
A CONTINUACIÓN SE PRESENTA UNA GUÍA DE TRABAJO PARA PODER VER ESTA GUÍA DEBE HACER CLIC DONDE SE PRESENTE EL ARCHIVO, TAMBIÉN PODRÁS VER UN VÍDEO DE AYUDA PARA EL DESARROLLO DE ESTA GUÍA.
DEBERÁS DESARROLLAR LA GUÍA EN TU CUADERNO O DESCARGARLA
AHORA DESCARGA LA GUÍA DE TRABAJO
La guía debes desarrollarla en el cuaderno o si descargas la guía en la guía
GUÍA Nº5 RACIONALZAR
OA1 Realizar cálculos y estimaciones
que involucren operaciones con números reales:•Utilizando la descomposición
de raíces y las propiedades de las raíces.
•Combinando raíces con números racionales.
• Resolviendo problemas que involucren estas operaciones en contextos diversos.
Indicadores de Evaluación: Operan con números racionales e irracionales
Utilizan la
descomposición de raíces y las propiedades de las raíces.
A continuación se presenta dos vídeos que te permitirán desarrollar la guía que Nº 5 que consiste en racionalizar una expresión fraccionaria, lo que significa es dejar la expresión sin raíz en el denominador (abajo) de la fracción.
Revisa la guía nº5 que se presenta ahora
En la guía que se presenta a continuación es de racionalizar expresiones radicales, desarrolla la guía en tu cuaderno y luego envía tus respuestas o tu apreciación de la guía, recuerda debes contestar para saber que revisaste o respondiste o intentaste resolverla o consultas, esa respuesta me permite saber que te llega la información.
Recuerda intenta resolverla lo que tu puedas
A continuación envía tus datos y respuestas o apreciación de la guía si fue fácil o difícil o consultas.
Recuerda contestar tu respuesta es importante para mi, gracias
GUÍA Nº 6 LOGARITMOS
OA2 Mostrar que comprenden las relaciones entre potencias, raíces enésimas y logaritmos:• Comparando representaciones de potencias de exponente racional con raíces enésimas en la recta numérica. • Convirtiendo raíces enésimas a potencias de exponente racional y viceversa. • Describiendo la relación entre potencias y logaritmos. • Resolviendo problemas rutinarios y no rutinarios que involucren potencias, logaritmos y raíces enésimas.
Indicadores de evaluación:- Explican la relación entre potencias y logaritmos. -Convierten desde un tipo de registro a otro; es decir, desde potencias a raíces y viceversa, y desde potencias a logaritmos y viceversa.
Logaritmos
Los logaritmos fueron introducidos por John Napier a principios del siglo XVII como un medio de simplificación de los cálculos. Estos fueron prontamente adoptados por científicos, ingenieros, banqueros y otros para realizar operaciones fácil y rápidamente, usando reglas de cálculo y tablas de logaritmos.
En análisis matemático, usualmente, el logaritmo de un número real positivo en una base de logaritmo determinada es el exponente al cual hay que elevar la base para obtener dicho número.
El logaritmo se abrevia como log
A CONTINUACIÓN SE PRESENTA UN VÍDEO PARA QUE TE AYUDE A RESOLVER LA GUÍA
ESPECIALMENTE LA PRIMERA PARTE
A continuación haz click para desarrollar la guía n°6 esta guía es de alternativa para que puedas enviar tus respuestas de manera más fácil, sin olvidar el desarrollo en el cuaderno
Logaritmo Guía Nº7
.OA2 Mostrar que comprenden las relaciones entre potencias, raíces enésimas y logaritmos:• Comparando representaciones de potencias de exponente racional con raíces enésimas en la recta numérica. • Convirtiendo raíces enésimas a potencias de exponente racional y viceversa. • Describiendo la relación entre potencias y logaritmos. • Resolviendo problemas rutinarios y no rutinarios que involucren potencias, logaritmos y raíces enésimas.
Indicadores de evaluación:- Explican la relación entre potencias y logaritmos. -Convierten desde un tipo de registro a otro; es decir, desde potencias a raíces y viceversa, y desde potencias a logaritmos y viceversa.
A continuación aprenderemos a resolver un logaritmo sin olvidar lo aprendido la sesión anterior porque esto nos ayudará a resolver un logaritmo
Recordemos: Como cambiamos de potencia a logaritmo

A continuación se presenta un vídeo para que entiendas como se calcula el valor de un logaritmo.
Una vez observado el vídeo se presenta la guía nº 7 para que la puedas resolver, para esto puedes resolverla en la guía o en tu cuaderno, sin olvidar los pasos que se presentan en la guía:
1º Transformar el logaritmo a potencia
2º Revisar la potencia que nos queda para ver cual es la incógnita.
3º Encontrar el valor.
Haz clic para descargar la guía nº 7 y resolver.
Ahora que ya resolviste la guía de trabajo puedes enviar tus respuestas indicando el número del ejercicio y la respuesta de este, no te olvides el desarrollo se realiza en tu cuaderno, posteriormente la corregiremos.
GUÍA Nº 8 CALCULAR LOGARITMOS (MAYO 18-22)
OA1 Realizar cálculos y estimaciones que involucren operaciones con números reales:•Utilizando la descomposición de raíces y las propiedades de las raíces.
•Combinando raíces con números racionales.
• Resolviendo problemas que involucren estas operaciones en contextos diversos.
Indicadores de Evaluación: Operan con números racionales e irracionales
Utilizan la descomposición
de raíces y las propiedades de las raíces.
A continuación se presentan las propiedades de logaritmos
Esto nos permitirá desarrollar nuestra guía de trabajo:

Estas propiedades te servirán para calcular logaritmos, te presentaré un vídeo que te permitirá entender de mejor manera el calculo de logaritmos y la aplicación de las propiedades.
Una vez visto el vídeo espero puedas desarrollar la guía que se presenta a continuación. Haz clic para descargar la guía
Si ya realizaste la guía de trabajo en esta o en tú cuaderno, puedes contestar el formulario de comunicación, para saber como te fue con ella.
Recuerda todo este proceso es importante para tu aprendizaje, gracias por esforzarte en el desarrollo de esta guía. Si tienes dificultad comunícate con migo por este medio u otro medio.
Lo importante es comunicarte, gracias por preocuparte de trabajar en la asignatura.
GUÍA Nº 9 PROPIEDADES DE LOGARITMOS(MAYO 25 AL 29)
OA2: Mostrar que comprenden las relaciones entre potencias, raíces enésimas y logaritmos:• Comparando representaciones de potencias de exponente racional con raíces enésimas en la recta numérica. • Convirtiendo raíces enésimas a potencias de exponente racional y viceversa. • Describiendo la relación entre potencias y logaritmos. • Resolviendo problemas rutinarios y no rutinarios que involucren potencias, logaritmos y raíces enésimas.
Indicadores de evaluación:- Explican la relación entre potencias y logaritmos. -Convierten desde un tipo de registro a otro; es decir, desde potencias a raíces y viceversa, y desde potencias a logaritmos y viceversa.
Recordemos que la sesión pasada estuvimos trabajando con las propiedades de logaritmos en el calculo de estos. Ahora trabajaremos las propiedades en expresiones algebraicas.
A continuación te presento un vídeo que te ayudará a resolver la guía nº 9 de aplicación de propiedades.
Una vez observado el vídeo espero te ayude para resolver la guía nº 9, recuerda la puedes resolver en tu cuaderno o en la guía . Cuando la termines puedes enviar las respuestas en el formulario o por fotos a mi wasapp, así podremos mantener contacto y aclarar dudas.
GUÍA 10 LOGARITMOS (01-05 JUNIO)
OA2 Mostrar que comprenden las relaciones entre potencias, raíces enésimas y logaritmos:• Comparando representaciones de potencias de exponente racional con raíces enésimas en la recta numérica. • Convirtiendo raíces enésimas a potencias de exponente racional y viceversa. • Describiendo la relación entre potencias y logaritmos. • Resolviendo problemas rutinarios y no rutinarios que involucren potencias, logaritmos y raíces enésimas.
Indicadores de evaluación:- Explican la relación entre potencias y logaritmos. -Convierten desde un tipo de registro a otro; es decir, desde potencias a raíces y viceversa, y desde potencias a logaritmos y viceversa.
Recordemos que las sesiones anteriores viste como calcular logaritmos, como aplicar sus propiedades en ejercicios y en expresiones algebraicas.
A continuación veremos un vídeo de logaritmos que nos ayudará a recordar lo aprendido o a reforzar este aprendizaje, si es necesario puedes revisar las actividades o vídeos anteriores también.
Ahora estamos en condiciones de resolver la guía presentada , en el cuaderno o en la guía, pero recuerda si tienes dificultades comunícate por el correo o por wasapp.
Una vez resuelta la guía puedes enviar tus respuestas por el formulario de contacto, recuerda lo importante de tu comunicación para el registro de trabajo individual.
GUÍA Nº 11 FUNCIÓN CUADRÁTICA ( 22 al 27 Junio)
OA3 Resolver, de manera concreta, pictórica y simbólica o usando herramientas tecnológicas, ecuaciones cuadráticas de la forma: •ax2 = b • (ax + b)2= c • ax2 + bx = 0 • ax2 + bx = c (a, b, c son números racionales, a ≠ 0).
Indicadores de evaluación: Resuelven algebraicamente las ecuaciones cuadráticas mediante varios métodos, como factorizar, completar al cuadrado y aplicar la fórmula.
Definición de función cuadrática. Se llama función cuadrática a la función matemática que se puede expresar como una ecuación que tiene la siguiente forma: f (x) = ax^2 + bx + c. En este caso, a, b y c son los términos de la ecuación: números reales, con a siempre con valor diferente a 0.(debe ser 0 para que no desaparezca el término x^2 y deje de ser cuadrática)(el exponente dos de la x hace que sea cuadrática).
Para iniciar esta unidad de álgebra recordaremos ecuación de primer grado y luego recordaremos productos notables y resolveremos ecuación cuadrática para entender la función cuadrática.
A continuación se presenta la guía de trabajo que puedes descargar haciendo clic y desarrollar en el cuaderno o en la guía si la puedes imprimir.
Una vez resuelta la guía debes enviar las respuesta de las actividades solicitadas en la guía por el formulario de contacto, colocando el número de la actividad y la respuesta que corresponda.
GUÍA N° 12 FUNCIÓN CUADRÁTICA ( 06- 10 JULIO)
OA3 Resolver, de manera concreta, pictórica y simbólica o usando herramientas tecnológicas,
ecuaciones cuadráticas de la forma: •ax2 = b
• (ax + b)2= c • ax2 + bx = 0 • ax2 + bx = c (a, b, c son números racionales, a ≠ 0).
Indicadores de evaluación: Resuelven algebraicamente las ecuaciones cuadráticas mediante varios métodos, como factorizar, completar al cuadrado y aplicar la fórmula.
A continuación un recordatorio de los productos notables y de las factorizaciones para que puedas resolver la guía de aprendizaje.

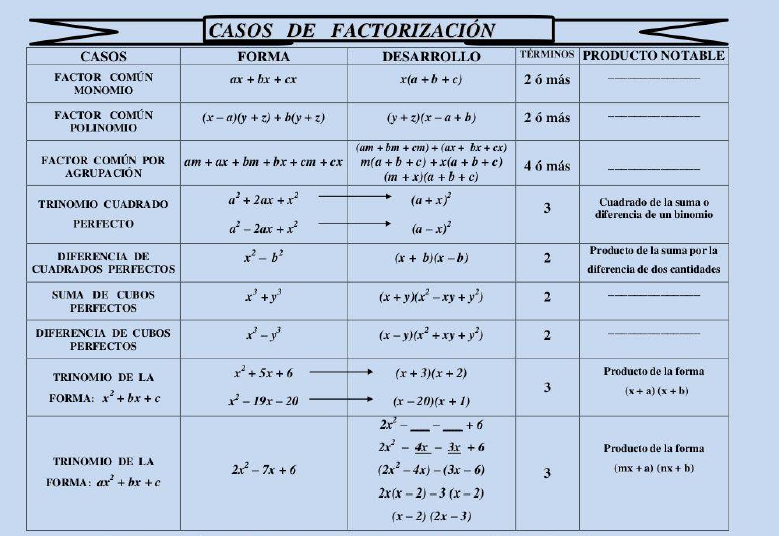
A continuación se presenta la guía de aprendizaje para que la resuelvas en tu cuaderno o si puedes imprimir en la guía.
También puedes descargar la misma guía pero con adecuación curricular
Una vez resuelta la guía puedes enviar tus respuestas a través de el formulario de contacto, no olvides comunicarte para que quede registro de tu trabajo personal.
GUÍA 13 (03-14 agosto)
U2:OA3: Mostrar que comprenden la función cuadrática f(x) = ax2 +bx + c: (a ≠ 0)• Reconociendo la función cuadrática f(x) = ax2 en situaciones de la vida diaria y otras asignaturas.• Representándola en tablas y gráficos de manera manual y/o con software educativo.• Determinando puntos especiales de su gráfica.• Seleccionándola como modelo de situaciones de cambio cuadrático de otras asignaturas, en particular de la oferta y demanda.
Función Cuadrática
¿Qué es una función cuadrática?
Definición de función cuadrática. Se llama función cuadrática a la función matemática que se puede expresar como una ecuación que tiene la siguiente forma:
f (x) = ax2 + bx + c. En este caso, a, b y c son los términos de la ecuación: números reales, con a siempre con valor diferente a 0.(debe ser 0 para que no desaparezca el término x2 y deje de ser cuadrática)(el exponente dos de la x hace que sea cuadrática).
A continuación se presenta un vídeo de apoyo para lo revises y puedas resolver la guía de aprendizaje.
Una vez observado el vídeo puedes desarrollar la guía de aprendizaje en tu cuaderno, recuerda que ese desarrollo es tu bitácora de trabajo, también si tienes la posibilidad de imprimir la guía puedes desarrollarla en ella.
Una vez resuelta la guía debes comunicarte para saber de tu avance, por este medio o por otro medio de contacto. Puedes llenar el formulario de contacto con tus respuestas o sólo informar de tu avance y desarrollo, es fundamental.
FUNCIÓN CUADRÁTICA
U2:OA3:Mostrar que comprenden la función cuadrática f(x) = ax2 +bx + c: (a ≠ 0)• Reconociendo la función cuadrática f(x) = ax2 en situaciones de la vida diaria y otras asignaturas.• Representándola en tablas y gráficos de manera manual y/o con software educativo.• Determinando puntos especiales de su gráfica.• Seleccionándola como modelo de situaciones de cambio cuadrático de otras asignaturas, en particular de la oferta y demanda.
Indicadores de Evaluación: Reconocen representaciones de la función cuadrática en curvas de la vida cotidiana (balísticas, caída de pelotas, caída de agua, etc.).• Grafican funciones cuadráticas a partir de una tabla de valores en la cual están dados los diferentes parámetros a, b, c.
Se presenta un vídeo de reconocer una función y luego graficarla, la primera parte te servirá para desarrollar la guía
A continuación se presenta la guía de trabajo número 14